Dynamic Programming
BACK: Divide and Conquer
When I first heard about dynamic programming, I thought it was going to be a really cool programming technique that would change the code as it runs. I was greatly disappointed when it just meant that we’re storing solutions to our subproblems in some table. Essentially, when we recursively call a function over and over again, we might run into some of the same subproblems. Instead of solving it all over again, why not just keep that memoized somewhere?
For example, fibonacci. We can draw out the recursive tree of Fib(5) as so:
If we ran a normal fibonacci recursive code, we can see how many times we calculate for the same fibonacci number on the table on the right. That’s a lot of recursive calls (with bigger n) for the same solutions. Dynamic programming seeks to fix that.
Rod Cutting Problem
The rod cutting problem asks us: If I have a rod of length \(n\) and different rods will sell for different prices, what is the best way to cut the rod so that we can maximize our profit? i.e: If I have a rod of size 4, I could sell the rod as is, in 3 and 1, or as 2 and 2.
There is a recursive pseudocode solution to this problem on page 363, but if we analyze this, the runtime will be \(O(2^n)\). Let’s draw out the recursive tree to see what’s being calculated.
Similarly to the fibonacci recursive tree, we can see that we are calculating the same thing over and over again. So why not just save the time and store the sub-solutions into a table?
We can then implement a top down (starting with \(n = 4\)) solution (pg 355-366) or a bottom up (starting with \(n = 0\)) solution (pg 366). Either way, I recommend filling out a table and drawing this problem out on a whiteboard to see the process of the code.
ex: TBD
Matrix Chain Multiplication Problem
Matrix Chain Multiplication tries to find the most optimal way to multiply matrices together to minimize the number of operations that we perform. It tells us where to draw our parentheses. You can see more about the pseudocode and how to draw the parentheses by creating two separate upper triangular matrices, but here I’m just going to explain the dynamic-programmingness of it.
Similarly to the other rod cutting and fib, if we take the recursive solution (pg 374), we can draw out a tree of what it looks like when we let it play out recursively: big and ugly.
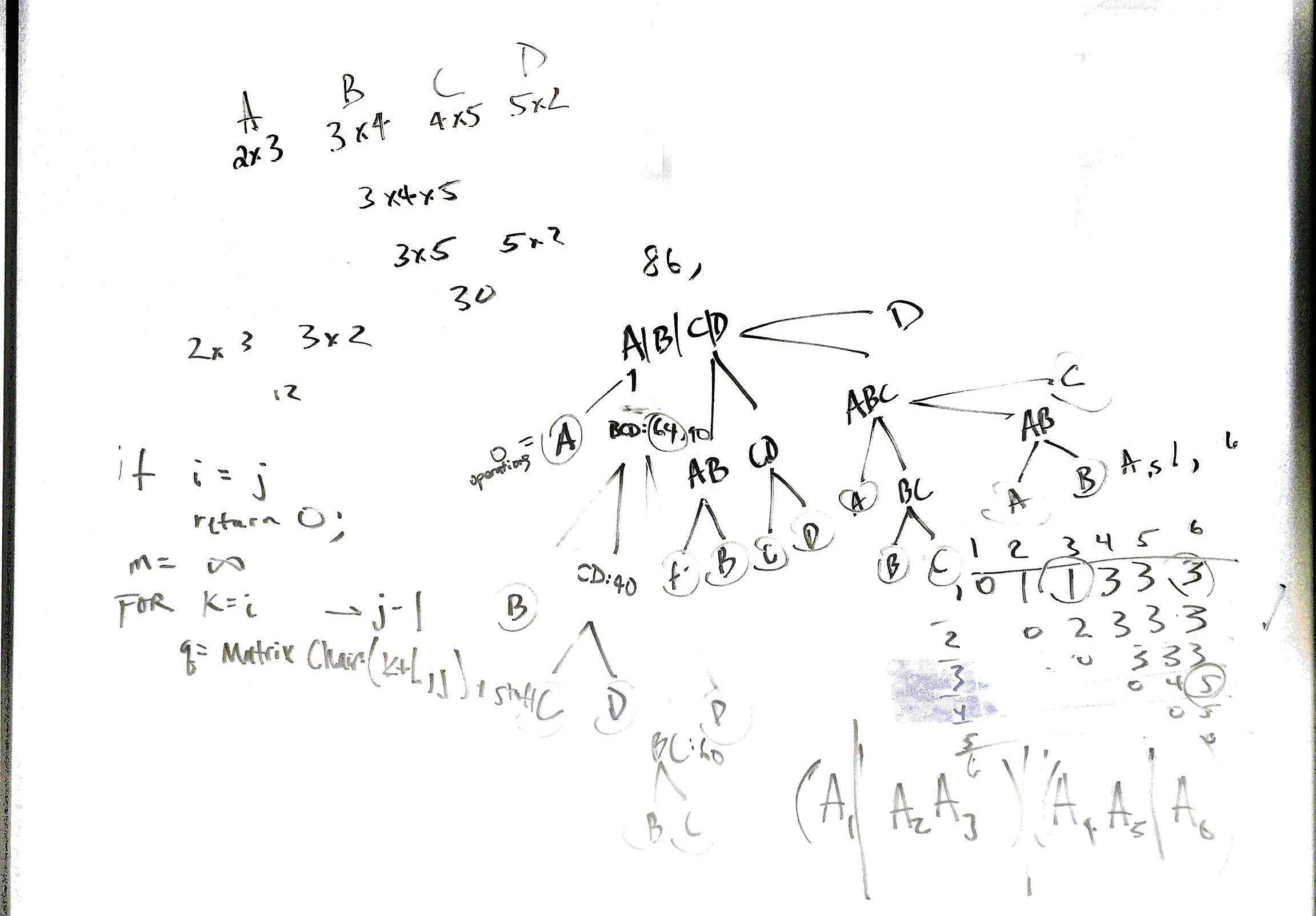
Rather than doing this, we can store our sub solutions into those two matrices found on pg 376.
more explanation TBD, but here’s a worked out example (thanks Yiying)

Longest Common Subsequence Problem
LCS solves: In two different strings, what is the longest common sequence between them (doesn’t have to be consecutive, just in order)? ie: in AZBZCZDZEZ and ABCDEFGH, the LCS would be ‘ABCDE’ or 5 characters.
We can first determine a recursive solution (pg 393) (notice a pattern yet?) and then determine that we would make the algorithm more optimal by memoizing the solutions.
explanation TBD, but here’s a worked out example (thanks Yiying)