Statistical Learning
BACK: Table of Contents
UNDER HEAVY CONSTRUCTION: NOT EVERYTHING MAY BE CORRECT.
A good way to think about this class: \(Y = f(X) + \varepsilon\)
Here, we see \(Y\) as something that we want to find out: the sales of a product, the classification of an image, etc, which is a dependent variable upon \(X\). Here, \(X\) represents the features,inputs, independent variables that \(Y\) is dependent upon. Based on the values of \(X\), our \(Y\) will vary, assuming that there is a relationship between the two variables. We also want to consider the error of our relationship (assuming that we aren’t able to find a perfect model \(f(X)\)).
Consider the Advertising example that is also included in the textbook.
Here, we want to predict sales (\(Y\)) based on the features of the Advertising dataset. The budget spent on TV (\(X_1\)), Radio (\(X_2\)), Newspaper (\(X_3\)). The blue line showed in each graph is the model \(f(X_n)\) that tries to predict the amount of sales based on feature \(X_n\). So how do we combine all the features together to make one ‘super’ model?
First, some definitions and reasoning about why we would want to do this:
- Prediction: Based on the values of \(X\), what is \(Y\)?
- Inference: What factors of \(X\) influence \(Y\) the most? For the Advertising example: Which \(X_n\) affect \(Y\) the most?
- Parametric Model: We assume something about the shape of \(f(X)\), i.e: The relationship between \(X\) and \(Y\) is linear.
- Non-Parametric Model: We do not make assumptions about the shape, and try to make some curvy shape to connect all the dots together (danger of over-fitting)
Another example: Since we are making an assumption about the general form of this equation, we can say that this is a parametric model:
\[income%20\approx%20\beta_0%20+%20\beta_1&*age&+\beta_2*education\]This might look something like this:
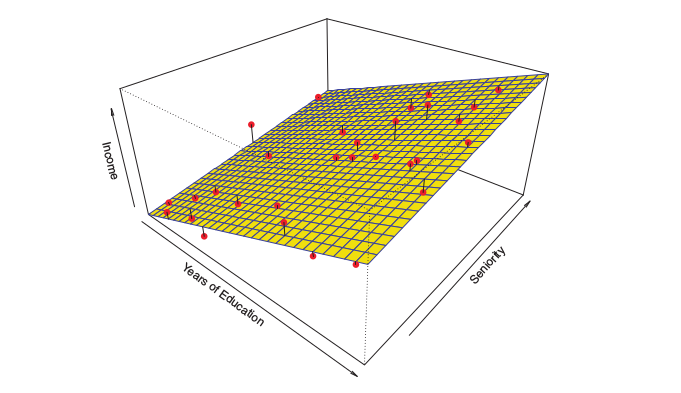
So the goal of this parametric model is to find the values of \(B_0\), \(B_1\), … to try to minimize the error or to find the best predictor of income (\(Y\)). Meanwhile, a non-parametric model might look something like this, where every point of the dataset touches the weird shape that we have made–there is ZERO error on this model.
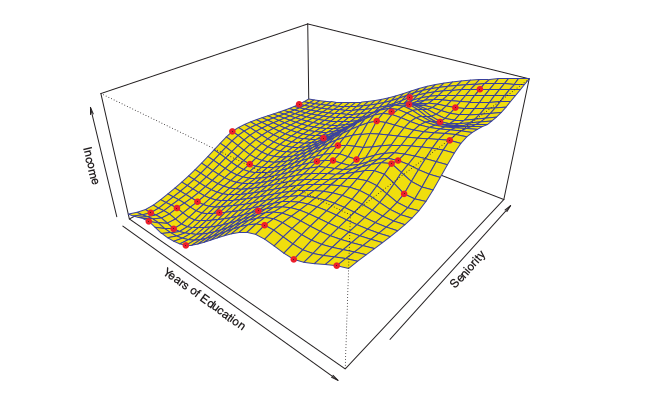
The problem with this is that there is a huge chance that any new data points will probably not match the general behavior of the model.
There is also the ideas of supervised and unsupervised learning. In supervised learning, we have information about all of our features (X) and our outputs (Y). In other words, we have a training dataset to work with. On the other hand, we do not have this information in unsupervised learning.
Cool. We have our model now, but how do we know if it’s a good model or not? We can take a look at the mean squared error. This is given by the equation
\[MSE=\frac{1}{n}\sum_{i=1}^{n}(y_i-\hat{y})^2\]We can use this equation by splitting our dataset into training and testing, so that we still have points that are available for us to verify if our model is accurate or not. This can be done through a simple ~80/20 split (training/testing) or a process called cross-validation, where we split the dataset into buckets and switch around with all the possible combinations of training/testing buckets and take some kind of average between all of them.
Alright, let’s take a look at some models for classification now:
Baye’s Classifier
Baye’s classifier is a classification tool that relies on knowing the probabilities and conditional probabilities of whatever you’re trying to classify. For example, is an email “spam” or “not spam”?
The video above uses this example and will scan the email for the words “viagara,” “prince,” and “Udacity.” They estimate the probabilities, which is how we generally obtain these probabilities, which makes Naive Baye’s classifier not the best classification tool. We’re essentially just applying Baye’s Theorem here, which was covered in Math 032 and every other stats class, so let’s take a look at a different algorithm.
K-Nearest Neighbor
K Nearest Neighbors is super intuitive! In a dataset, if I have a dataset with labeled classes and then I have a new point, it’s intuitive to say, “Oh, the closest point is the same class as the new point.” Obviously, this won’t always work–what if my new point is right next to a noisy point that overlaps into a different class? So we can take a look at the 2 or 3 or 4 nearest neighbors.
Check out this Python Notebook for additional explanation.
But how do we choose what value of K to use? This is a hyperparameter–it really just depends on the situation. By using cross validation, we are able to pick different values of K and then compare each model to each other with the goal of minimizing some statistic (AIC, BIC, MSE, etc.)